Khái niệm hình tam giác
Tam giác hay hình tam giác là một loại hình học cơ bản trong đó ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh. Đặc trưng quan trọng của tam giác là tổng ba góc trong một tam giác phải luôn bằng 180 độ.
Tam giác luôn luôn là một đa giác đơn và luôn là một đa giác lồi tức là các góc trong hình tam giác luôn nhỏ hơn 180 độ. Một tam giác có các cạnh AB, BC và AC được gọi là tam giác ABC.
Các tính chất cơ bản của hình tam giác
Theo tính chất về góc của hình tam giác, tổng ba góc trong một tam giác luôn bằng 180 độ. Ví dụ: Ta ký hiệu các góc trong tam giác là A, B và C, thì A + B + C = 180 độ.
Tính chất về cạnh của hình tam giác hay còn được gọi là bất đẳng thức tam giác quy định, tổng độ dài hai cạnh của tam giác luôn lớn hơn độ dài cạnh còn lại. Điều này có thể được biểu diễn như sau: a + b > c, b + c > a, c + a > b. (Trong đó: a, b, c lần lượt là các cạnh của một hình tam giác.)
Hai tam giác được gọi là bằng nhau (hay đồng dạng) khi các cạnh và các góc của chúng tương ứng bằng nhau. Điều này có nghĩa là các cặp cạnh tương ứng của hai tam giác có độ dài bằng nhau và các cặp góc tương ứng cũng có giá trị bằng nhau.
Hình tam giác có ba đường cao - các đường vuông góc với các cạnh và đi qua các đỉnh tương ứng và ba đường trung tuyến - các đường nối các đỉnh với trung điểm của các cạnh tương ứng.
Các loại hình tam giác thường gặp
Hình tam giác được phân thành nhiều loại dựa trên đặc điểm của các cạnh và các góc. Cụ thể như sau:
Tam giác nhọn
Tam giác nhọn là loại tam giác cơ bản nhất với độ dài các cạnh khác nhau và số đo góc trong cũng không giống nhau. Tất cả ba góc của tam giác đều nhọn, tức là có giá trị nhỏ hơn 90 độ.
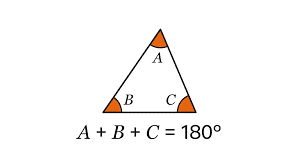
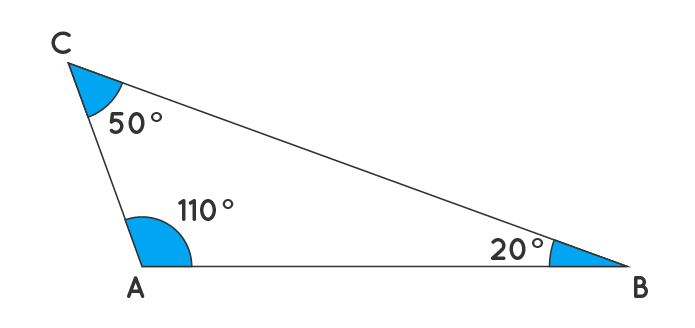
Tam giác tù
Tam giác tù là tam giác có một góc tù, tức là một góc trong có giá trị lớn hơn 90 độ hay một góc ngoài bé hơn 90 độ.
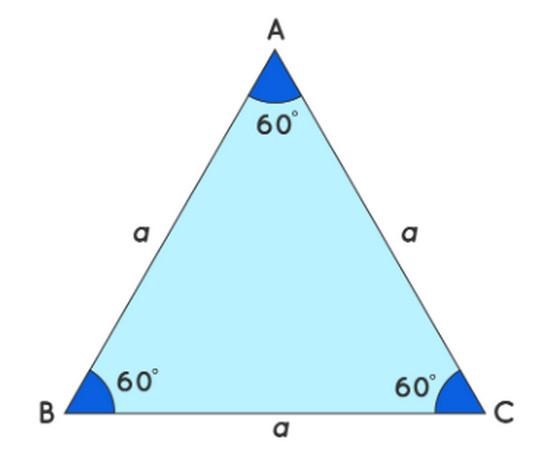
Tam giác đều
Tam giác đều là tam giác có cả ba cạnh và ba góc bằng nhau. Tất cả các góc trong tam giác đều đều có giá trị 60 độ.
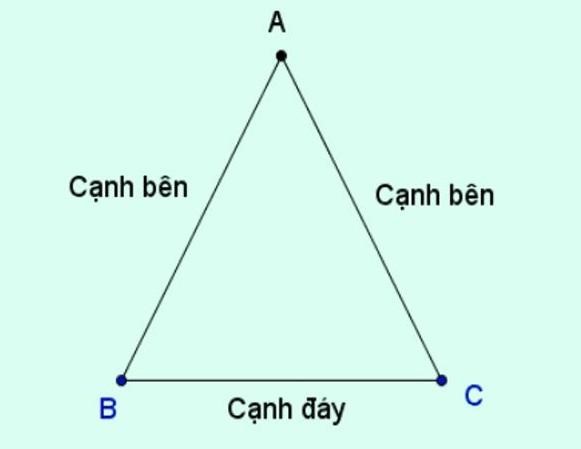
Tam giác cân
Tam giác cân là tam giác có ít nhất hai cạnh bằng nhau. Điều này đồng nghĩa với việc có ít nhất hai góc bằng nhau.
Tam giác vuông
Tam giác vuông có một góc vuông, tức là một góc có giá trị chính xác là 90 độ.

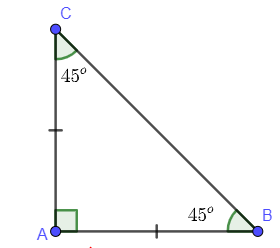
Tam giác vuông cân
Tam giác vuông cân là tam giác có một góc vuông và hai cạnh gần vuông bằng nhau.
Cách tính diện tích theo từng loại hình tam giác
Tùy vào từng loại hình hình tam giác, chúng ta sẽ có những công thức khác nhau được sử dụng. Dưới đây là một số công thức thường gặp, dễ hiểu và được sử dụng nhiều nhất có thể tham khảo và áp dụng vào giải bài tập
Công thức tính diện tích tam giác nhọn
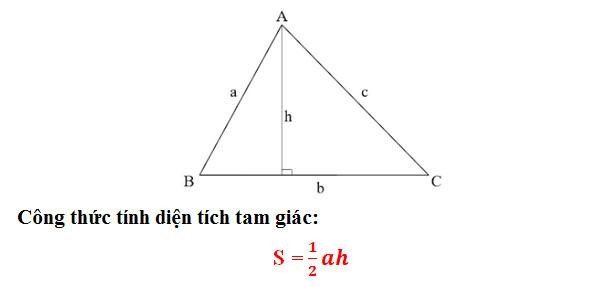
S = (a x h)/2
Diện tích của tam giác nhọn được tính bằng cách nhân chiều cao (h) với độ dài của đáy (a), sau đó lấy kết quả chia cho hai. Hay có thể hiểu một cách khác rằng diện tích tam giác thường sẽ bằng ½ tích của chiều cao với chiều dài cạnh đáy của tam giác.
Công thức trên cũng được áp dụng đối với các loại tam giác tù, tam giác cân và tam giác đều trong khi giải bài tập liên quan.
Ví dụ:
Tính diện tích hình tam giác có độ dài đáy là 6m và chiều cao là 30dm.
Lời giải: Chiều cao 30dm = 3m
Diện tích tam giác là
S=(6 x 3)/2 = 9 (m2)
Công thức tính diện tích tam giác vuông
Tam giác vuông là tam giác có 1 góc vuông 90 độ. Về cách tính diện tích của tam giác vuông cũng sẽ bằng ½ tích của chiều cao với chiều dài đáy. Nhưng vì tam giác vuông có 2 cạnh góc vuông, nên chiều cao sẽ ứng với 1 cạnh góc vuông, cùng với chiều dài đáy sẽ ứng với cạnh góc vuông còn lại.
Từ đó, ta có công thức tính diện tích tam giác vuông:
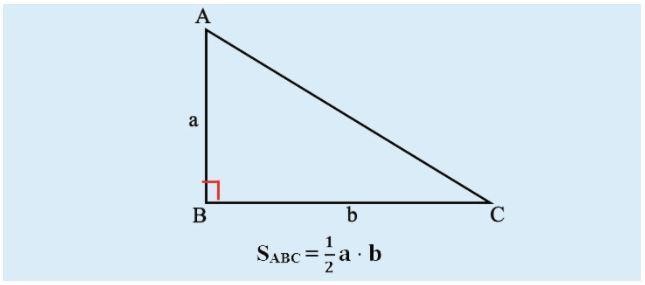
S = (a x b)/ 2
Trong đó a, b là độ dài hai cạnh góc vuông
Ví dụ: Tính diện tích của tam giác vuông có hai ai cạnh góc vuông lần lượt là 5cm và 6cm
Lời giải:
Diện tích của hình tam giác là:
(5 x 6) : 2 = 15 (cm2)
Công thức tính diện tích tam giác vuông cân
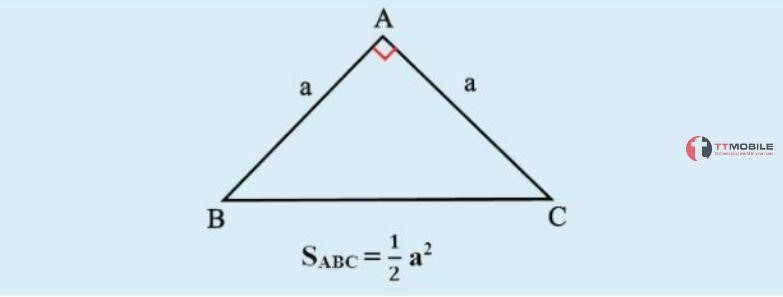
Tam giác vuông cân là tam giác vừa vuông, vừa cân. Như hình vẽ, cho tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông.
Dựa vào công thức tính tam giác vuông cho tam giác vuông cân, với chiều cao và cạnh đáy bằng nhau. Ta có công thức:
S = 1/2 x a2
Công thức tính diện tích tam giác trong hệ tọa độ Oxyz
Trên lý thuyết, ta có thể dùng các công thức tính tam giác phẳng cho tam giác trong không gian Oxyz. Nhưng như vậy sẽ gặp nhiều khó khăn khi tính toán. Vậy nên, trong không gian Oxyz, ta sẽ tính diện tích tam giác dựa vào tích có hướng.
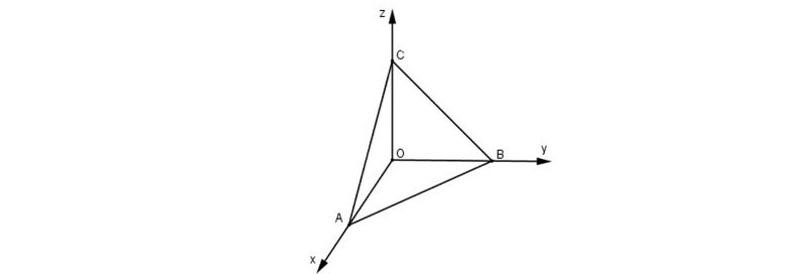
Diện tích tam giác trong hệ tọa độ Oxyz được tính theo công thức sau:

Ví dụ: Trong không gian Oxyz, cho tam giác ABC có tọa độ ba đỉnh lần lượt là A(-1;1;2), B(1;2;3), C(3;-2;0). Tính diện tích tam giác ABC.
Lời giải:

Xem thêm: Bài toán Tiểu học đếm hình tam giác tưởng "dễ như ăn kẹo", kết quả lại là "cú lừa" của cô giáo
Bài toán đếm hình lớp 1 đơn giản, nhưng lời giải của học sinh khiến mọi người cảm thấy 'hack não'
Bí quyết giúp học, ghi nhớ kiến thức diện tích tam giác hiệu quả
Khả năng tập trung là một trong những yêu cầu quan trọng để có thể ghi nhớ công thức tính diện tích hình tam giác cũng như các công thức toán học khác một cách hiệu quả.
Nếu giữ được sự tập trung vào một vấn đề ngay cả khi xung quanh đang ồn ào sẽ giúp bạn có một trí nhớ tốt, giúp người học ghi nhớ nhanh cả những công thức toán học vốn rất khô khan. Để có sự tập trung đó mỗi cá nhân đều cần thay đổi những thói quen hàng ngày, tập trung cao độ vào công thức muốn ghi nhớ.

Ngoài ra, học sinh sẽ ghi nhớ tốt những điều mà bản thân đã hiểu rõ ràng. Nếu đọc nhiều lần mà không hiểu một công thức toán học nào đó hãy dùng biện pháp nhớ “cưỡng chế”, tức là cứ học thuộc nội dung và sau đó từ từ tìm hiểu những gì mình nhớ được. Người học cũng có thể nhờ bạn bè, thầy cô giảng giải hoặc có thể tìm ở những tài liệu khác cho đến khi hiểu những nội dung của công thức đó.
Tuy nhiên, nếu chỉ học trên sách vở, lý thuyết thì trẻ rất dễ nhanh quên các công thức tính toán. Chính vì vậy, việc thực hành thường xuyên là rất cần thiết để giúp ghi nhớ, áp dụng kiến thức một cách hiệu quả hơn.
Việc thực hành ở đây có thể là làm bài tập trong sách giáo khoa, tìm hiểu thêm nhiều thông tin trên internet để luyện tập, tham khảo nhiều kiến thức nâng cao, tham gia các trò chơi, cuộc thi liên quan, học nhóm cùng bạn bè,…
Luyện tập thường xuyên, học sinh sẽ dễ dàng ghi nhớ được kiến thức mình đã được học, biết cách áp dụng vào thực tế và đặc biệt là hình thành tư duy sáng tạo trong quá trình học tập hiệu quả hơn.
Các dạng bài tập tính diện tích hình tam giác từ cơ bản đến nâng cao
Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao
Đối với dạng bài tập này, đề bài thường sẽ cho dữ kiện về chiều cao và độ dài cạnh đáy. Nên các em chỉ cần áp dụng công thức tính tam giác thường để tìm ra đáp án chính xác.
Ví dụ: Tính diện tích tam giác thường và tam giác vuông có:
- a) Độ dài đáy bằng 30cm và chiều cao bằng 25cm.
- b) Hai cạnh góc vuông có độ dài lần lượt là 6dm và 4dm.
Lời giải:
- a) Diện tích hình tam giác là:
30 x 25 : 2 = 375 (cm2)
- b) Diện tích hình tam giác là:
6 x 4 : 2 = 12 (dm2)
Đáp số: a) 375cm2; b) 12dm2
Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao
Ở dạng bài tập này, dữ kiện đề bài sẽ cho biết thông số của chiều cao và diện tích hình tam giác, yêu cầu học sinh sẽ tính độ dài đáy. Nên từ công thức tính diện tích, ta suy ra công thức tính độ dài đáy: a = S x 2 : h
Ví dụ: Cho hình tam giác với diện tích bằng 480cm2, chiều cao là 60cm. Tính độ dài cạnh đáy bằng bao nhiêu?
Lời giải:
Độ dài cạnh đáy của hình tam giác là:
480 x 2 : 60 = 16 (cm)
Đáp số: 16cm
Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy
Cũng từ công thức tính diện tích của hình tam giác, ta cũng sẽ suy ra công thức tính chiều cao của hình như sau: h = S x 2 : a
Ví dụ: Cho hình tam giác, biết diện tích bằng 1025cm2, độ dài đáy bằng 50cm, tính chiều cao của hình tam giác đó.
Lời giải:
Chiều cao của hình tam giác là:
1025 x 2 : 50 = 41 (cm)
Đáp số: 41cm
Phương Uyên(T/h)




